Tipos de Funciones

Como nuestro primer tema para el blog, decidimos hablar de algo básico como lo son las funciones. Lo más esencial es conocer qué son, cómo clasificarlas y saber que tipo de funciones existen.

¿Qué es una función?

En matemática, una función es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).

Clasificación:

En este caso, nos enfocaremos en las más básicas que son las Lineales (en este caso llamadas de primer grado), las Cuadráticas, las Racionales y las Cúbicas (Una de las que se agrupan en las funciones exponenciales).

Funciones Lineales 

Una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta

Esta función se puede escribir como:
f (x) = mx + b

Ejemplos:

En este tipo podemos encontrar una subclasificación llamada Funciones Lineales de Varias Variables:

Las funciones lineales de varias variables admiten también interpretaciones geométricas. Así una función lineal de dos variables de la forma f (x,y) = a₁x + a₂y representa un plano y una función.

Funciones Cuadráticas

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida por:
y = ax² + bx + c

Graficación de Funciones Cuadráticas:

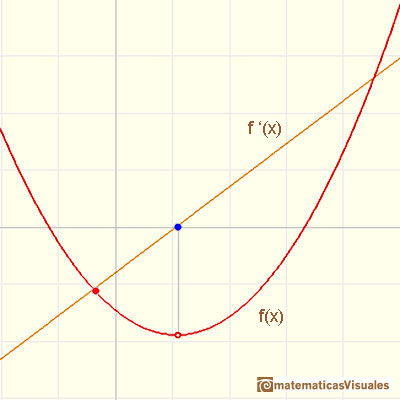
La funcion derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.

En este caso, f(x) es la función cuadrática y f'(x) es la función lineal derivada.

Funciones Racionales

En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma: 
f(x) = P(x)/Q(x)
donde P y Q son polinomios y x una variable

Ejemplo:

Propiedades:

• Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).

• Todas las funciones racionales cuyos coeficientes pertenecen a un cuerpo forman un cuerpo que incluye al cuerpo base como subcuerpo. El cuerpo de funciones funcionales racionales forma un subcuerpo del cuerpo de series de potencias formales.

Funciones Cúbicas

La función cúbica se define como el polinomio de tercer grado; el cual se expresa de la forma: f(x) = ax + bx +cx + d

Gráfica

Propiedades:

• El dominio de la función es la recta real, es decir (-a : a)
• El recorrido de la funcion, es decir, la imagen, es la recta real
• La función es simétrica respecto del origen, ya que f(-x) = -f(x)
• La función es continua en todo su dominio.
• La funcion es siempre creciente.
• La función no tiene asintotas.
• La función tiene un punto de corte con el eje Y.
• La funcipon puede tener hasta un máximo de 3 puntos de interección con el eje X.

Por el momento es todo, esperamos que hayan aprendido algo; Cualquier duda que les haya quedado no duden en escribirla en los comentarios, con gusto contestaremos lo que necesiten.

Saludos

Equipo MTMTC